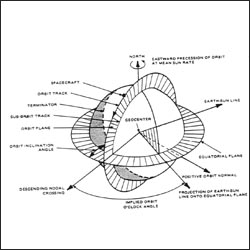
Source: Landsat-6 Programming and Control Handbook
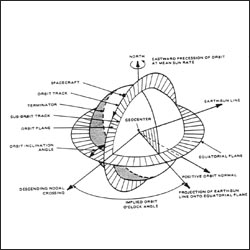
Schematic diagram illustrating the geometry of a sun-synchronous orbit for the morning descending node of Landsat.
This schematic appears in the Landsat 6 Programming and Control Handbook that was prepared by Martin Marietta Astro Space in 1993.
Like all of the Landsat satellites, Landsat 6 would have been in a sun-synchronous orbit had its launch been successful.
The L6 Handbook tells us, “for a nominal sun-synchronous orbit (i.e., one that precesses at a rate of 0.9856°/day or 360°/year), the scene and spacecraft illumination conditions vary throughout the year but repeat on a yearly cycle. The changes during the year occur because apparent Sun motion in the ecliptic plane is non-uniform, whereas the satellite orbit precession is uniform relative to the equatorial plane. The parameter that determines the actual illumination time histories is the orbit o’clock angle. This is the angle between the ascending or descending node and the “mean sun” vector. For a perfect unsynchronized orbit, the orbit o’clock angle remains constant. Furthermore, the Local Mean Sun Time (LMST) of the nodal crossing is the orbit o’clock angle. The relationship is shown in [this figure].”